Από τότε που οι Ελληνες φιλόσοφοι, οι Προσωκρατικοί και κυρίως ο Πυθαγόρας με το «Πάντα κατ’ αριθμόν γίγνονται», όρισαν τα μαθηματικά ως το κεντρικό μονοπάτι για την εξέλιξη της Δυτικής Σκέψης, η σχέση του ανθρώπου με τους αριθμούς υπήρξε ανέκαθεν το προγεφύρωμα και το έσχατο καταφύγιο για τις μεγάλες ανακαλύψεις. Eστω και αν για τον πολύ κόσμο τα μαθηματικά παραμένουν μία τραυματική εμπειρία των μαθητικών χρόνων από την οποία απομακρύνονται με την πρώτη ευκαιρία. Oμως, για όποιον έχει ζήσει έστω και μία φορά την εμπειρία της τέλειας αισθητικά λύσης ενός σύνθετου μαθηματικού προβλήματος, η ηδονή είναι αντίστοιχη με τη συγγραφή μιας μεγάλης ποιητικής σύνθεσης ή της ολοκλήρωσης ενός πίνακα ζωγραφικής. Ο Πλάτωνας υποστήριζε ότι τα μαθηματικά εκφράζουν το αποκορύφωμα της ομορφιάς. Δεν χωρά αμφιβολία λοιπόν ότι τα μαθηματικά θα έπρεπε να θεωρούνται ως μία μορφή τέχνης, μιας και σε κάθε τους έκφανση θα πρέπει να καλύπτεται και το αισθητικό ζητούμενο, η ομορφιά της ταραχώδους αρμονίας του σύμπαντος.
Πίσω από κάθε μαθηματικό λοιπόν κρύβεται ένας καλλιτέχνης. Η έρευνα και η μυστικιστική ενόραση ενός μαθηματικού που πασχίζει επί δεκαετίες να λύσει ένα πρόβλημα μοιάζει με την έμπνευση και τον οίστρο ενός καλλιτέχνη. Και όπως έχουν αποδείξει επιστημονικές έρευνες, εκπορεύονται και τα δύο από τα ίδια κέντρα του εγκεφάλου, ακολουθώντας τα ίδια ανεξερεύνητα μονοπάτια που το ανθρώπινο είδος αναζητά την αλήθειά του και τον τρόπο να την κοινοποιήσει στον Κόσμο. Δεν είναι τυχαίο άλλωστε που κάμποσες ταινίες του Χόλιγουντ, αλλά και η διαδεδομένη αντίληψη του κοινού, περιβάλλουν τους «τρελούς επιστήμονες» με την αύρα και την αίγλη αντίστοιχη με εκείνη των καλλιτεχνών.
Ο μαθηματικός χρησιμοποιεί τα ίδια εργαλεία με έναν καλλιτέχνη: τη φαντασία, τη διαίσθηση, τις εμμονές και τις υπερβάσεις του μέσου ανθρώπινου νου, για να δημιουργήσει κάτι υψηλό και -κυρίως- κάτι πολύ όμορφο. Για τον μαθηματικό, μια σωστή λύση ενός προβλήματος είναι πρώτα και πάνω από όλα μία αισθητικά όμορφη εικόνα. Ακόμα και αν έχει φτάσει στο σημείο να έχει δώσει τις σωστές απαντήσεις, γνωρίζει ότι πρέπει να ψάξει ακόμα βαθύτερα, ώστε η τελική εκδοχή της λύσης να είναι εκτός από μαθηματικά ορθή και αισθητικά άψογη. Τα μαθηματικά μοιάζουν με ποίηση χωρίς γράμματα ή -ακόμα ακριβέστερα- είναι μουσική με άλλες νότες. Και ο μαθηματικός είναι ένας δημιουργός που δίνει μορφή σε κάτι άυλο και άπιαστο για τους πολλούς, φωτίζοντας όπως και ο καλλιτέχνης τις πιο ανεξερεύνητες γωνιές της ανθρώπινης περιπέτειας.
Ο Πικάσο έλεγε ότι τέχνη είναι η εξάλειψη του περιττού. Και στις 6+1 εξισώσεις που επιλέξαμε μέσα από εκατοντάδες, τα μαθηματικά αποδεικνύουν ότι μέσα από την λιτότητα και την απόλυτη ακρίβεια των μέσων έκφρασής τους μπορούν να σταθούν και ως υψηλή τέχνη. Αποτελώντας πάντα το κλείσιμο του ματιού του Θεού προς τον άνθρωπο.
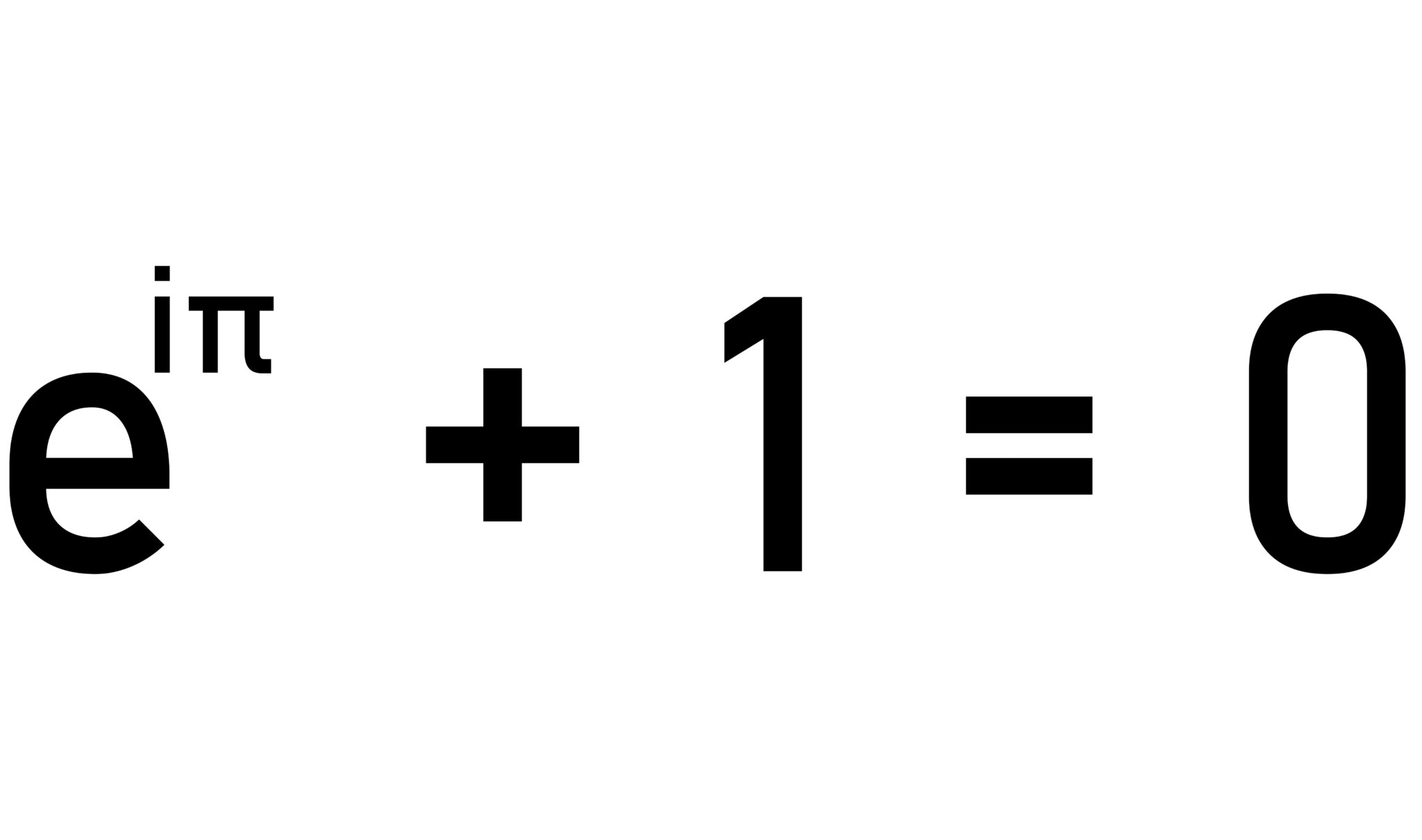
Η ταυτότητα του Όϊλερ
Για τους περισσότερους είναι ίσως η ομορφότερη αριθμητική πράξη που υπάρχει στον κόσμο. Πολλοί την παρομοιάζουν με ένα σονέτο του Σαίξπηρ, καθώς συνδυάζει ένα εκπληκτικό στιλιζάρισμα με μία βαθιά αίσθηση της μουσικότητας των αριθμών. Το εντυπωσιακό είναι ότι σε αυτή την εξίσωση βρίσκονται οι πέντε πιο βασικοί αριθμοί, το 0, το 1, το π, το λογαριθμικό e και ο φανταστικός αριθμός i (που είναι η τετραγωνική ρίζα του -1). Όλοι αυτοί ενώνονται σε ένα πανέμορφο σύμπλεγμα, που για πολλούς είναι το κόσμημα και η αισθητική κορύφωση των μαθηματικών. Ο Λέοναρντ Όϊλερ, που κάποιοι αποκαλούν και Μότσαρτ των εξισώσεων, υπήρξε μία από τις μεγαλύτερες μορφές στην ιστορία των μαθηματικών, γεννημένος στην Ελβετία τον 18ο αιώνα, ο οποίος παρέμεινε ενεργός μέχρι και τα τελευταία χρόνια της ζωής του, όντας για πάνω από 20 χρόνια τυφλός. Μάλιστα, όπως αναφέρεται, άφησε τόσο μεγάλο έργο πίσω του, που γίνονταν δημοσιεύσεις ακόμα και 30 χρόνια μετά τον θάνατό του.

Νόμος της παγκόσμιας βαρύτητας του Νεύτωνα
Μία αρχετυπική εξίσωση που έθεσε τα θεμέλια για την αντίληψή μας σχετικά με τον κόσμο και τα ουράνια σώματα και αποτελεί και σήμερα σημαντική κατάκτηση του ανθρώπινου πνεύματος, παρά το γεγονός ότι η θεωρία της σχετικότητας του Αϊνστάιν ανέτρεψε κάποια από τα συμπεράσματά της. Η εξίσωση αυτή είναι προϊόν μιας γενικότερης πνευματικής και επιστημονικής υπερδιέγερσης του 16ου αιώνα, όπου πολλά και σημαντικά ονόματα διατυπώνουν τις νέες θεωρίες που θα οδηγήσουν την ανθρώπινη σκέψη στη σύγχρονη εποχή. Δημοσιεύτηκε στις 5 Ιουλίου του 1687 στο έργο «Philosophiae Naturalis Principia Mathematica» και υποστηρίζει ότι δύο σώματα έλκονται από μία δύναμη ανάλογη της μάζας τους και αντιστρόφως ανάλογη του τετραγώνου της απόστασής τους. Εκτός από την αισθητική της αξία, τη χαρακτηρίζει και μία έντονη πνευματικότητα, καθώς είναι η πρώτη φορά που ο άνθρωπος ρίχνει κλεφτές ματιές στο εργαστήρι του Θεού και καθαρογράφει τα μυστικά του. Οπως και ο Μπαχ που ακολούθησε μέσω της μουσικής του.
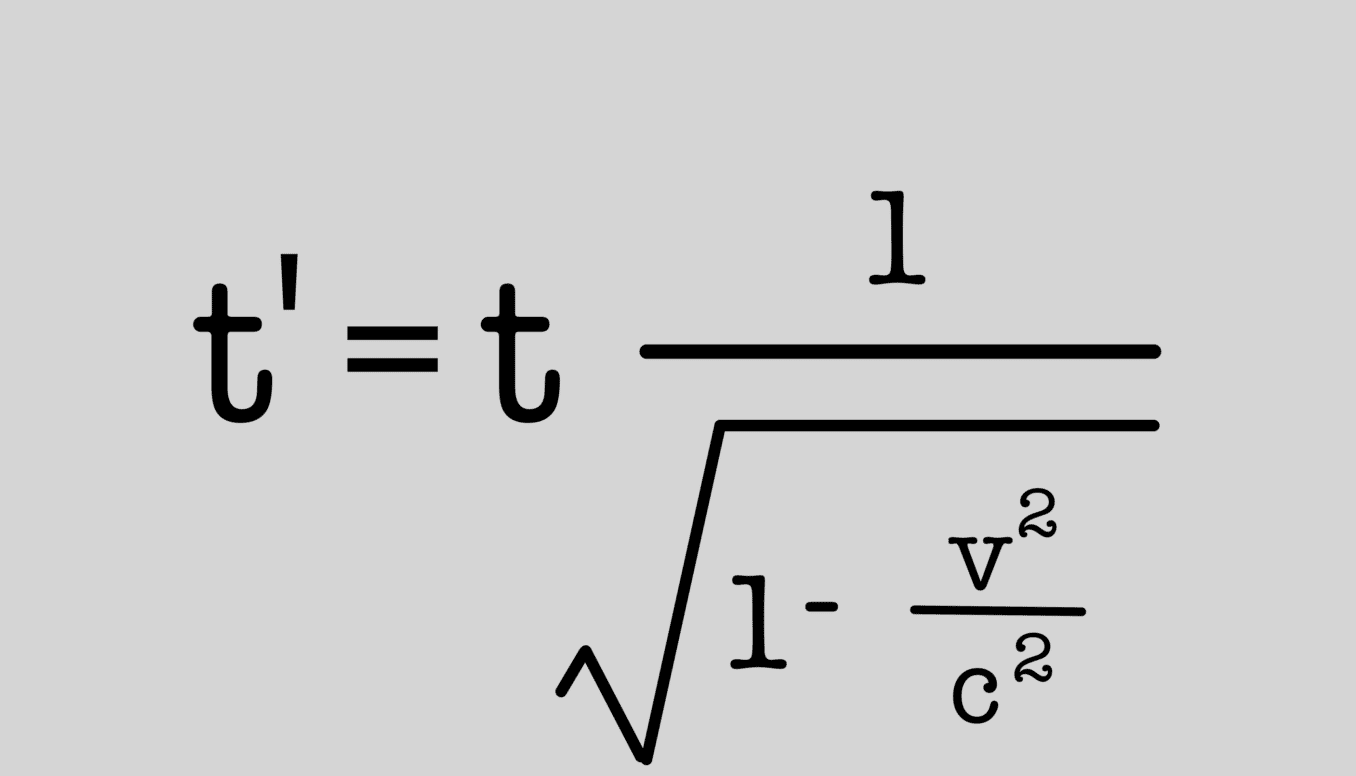
Εξίσωση της ειδικής σχετικότητας του Αϊνστάιν
Δεν είναι τυχαίο ότι η εμφάνιση της ειδικής θεωρίας της σχετικότητας το 1905 συμπίπτει με τις μεγάλες αλλαγές που φέρνουν τα νέα καλλιτεχνικά ρεύματα που αλλάζουν την αντίληψη του ανθρώπου για τα μέχρι τότε δεδομένα στην τέχνη. Υπό μία έννοια ο Αϊνστάιν είναι κάτι σαν τον Πικάσο της Φυσικής, αυτός που άλλαξε τον τρόπο με τον οποίο βλέπουμε τον κόσμο και τη θέση μας σε αυτόν. Ουσιαστικά ανοίγει ένα εντελώς νέο κεφάλαιο στην κατανόηση του κόσμου, πέρα από τον κόσμο των αισθήσεων, εκεί όπου ο χώρος και ο χρόνος είναι έννοιες σχετικές, υποστηρίζοντας ότι ο χρόνος μπορεί να διαστέλλεται ή να επιβραδύνεται, ότι ο άνθρωπος δεν είναι απλός παρατηρητής αλλά και ο ίδιος αντικείμενο παρατήρησης του σύμπαντος.
Αν όλα αυτά θυμίζουν τις τεράστιες δομικές αλλαγές που έφερε ο Πικάσο στη ζωγραφική και στον τρόπο που άλλαξε κάθε κατεστημένη αντίληψη για την απεικόνιση του κόσμου, απλά επιβεβαιώνει ότι η τέχνη των μαθηματικών και της Φυσικής ακολουθεί κοινή πορεία με τις υπόλοιπες τέχνες.

Η εξίσωση του Σρέντινγκερ
Αν και έμεινε γνωστός στον κόσμο της επιστήμης (και της τέχνης) με τη διάσημη πλέον «γάτα» του, ο Σρέντινγκερ διατύπωσε μία από τις αρχετυπικές εξισώσεις της σύγχρονης εποχής, η οποία αποτελεί τον κεντρικό πυλώνα της κβαντικής μηχανικής. Παρουσιάστηκε το 1926 και έδωσε στον δημιουργό της το Νόμπελ Φυσικής το 1933. Πρόκειται για μία όμορφη και ιδιαίτερα κομψή μαθηματική εξίσωση, η οποία -κατ’ αντιστοιχία με τα δραστήρια κινήματα τέχνης της εποχής της- φέρνει μία τεράστια αναστάτωση στα μέχρι τότε δεδομένα, εστιάζοντας στον τρόπο που λειτουργούν τα άτομα και τα υποατομικά σωματίδια, για να εξηγήσει τα κενά που είχαν αφήσει οι μέχρι τότε θεωρίες. Με βάση τις προσπάθειες του Σρέντινγκερ αναπτύχθηκε όλη κβαντική μηχανική, ανοίγοντας όμως παράλληλα πόρτες -όπως έκανε ο Έλιοτ με την «Ερημη χώρα» που είχε δημοσιευτεί λίγα χρόνια πριν- σε νέα μυστήρια και γόνιμες νέες ιδέες. Οσο για τη «γάτα» του, ακόμα κανείς δεν γνωρίζει με σιγουριά τι θα βρει όταν θα ανοίξει το κουτί.
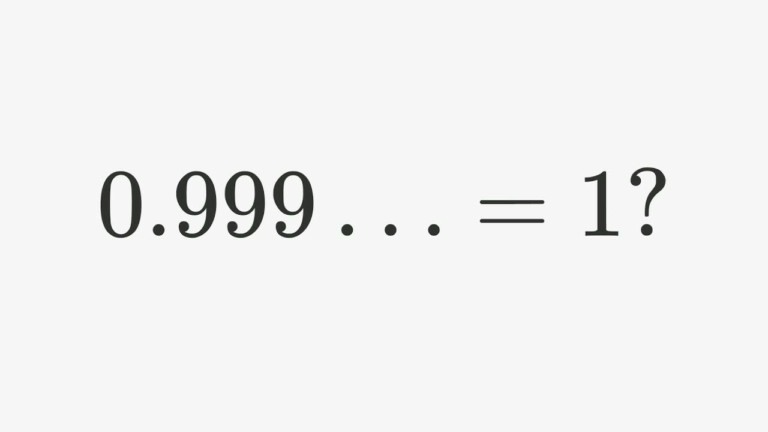
1=0,9999999999…..
Οταν τα μαθηματικά αφήνουν τον «γειωμένο» κόσμο των ξεκάθαρων αποδείξεων και μπαίνουν στα χωράφια της ποίησης και του τρόπου που εκείνη συνομιλεί με το ανέφικτο της ανθρώπινης σκέψης. Η ιδέα ότι το ένα μπορεί να εκφραστεί ως 0,999… ακολουθούμενο από μια άπειρη σειρά από εννιάρια, είναι μια πραγματικά όμορφη εξίσωση, που προκαλεί τα όρια της κατανόησης και της λογικής μας. Αυτή η εξίσωση μάς αναγκάζει να αμφισβητήσουμε ένα από τα θεμελιώδη αξιώματα που μεγαλώσαμε μαθαίνοντας: ότι δηλαδή 1=1.
Η αισθητική αξία της της συγκεκριμένης «εξίσωσης» έγκειται στο γεγονός ότι ισορροπεί τέλεια ανάμεσα στη μονάδα αριστερά και το άπειρο δεξιά, ενώ παράλληλα είναι απλή και κατανοητή από όλους. Ομως το ότι λειτουργεί υπονομευτικά και με τον τρόπο της ποίησης σε όλα όσα θεωρούμε δεδομένα, της δίνει δικαιωματικά μια θέση στις υψηλές στιγμές της καλλιτεχνικής διάστασης των μαθηματικών.

Η χρυσή τομή
Αποτελεί τον τύπο όπου τα μαθηματικά και η τέχνη βρίσκουν όσο πουθενά αλλού τον κοινό τους τόπο (και ίσως και την κοινή τους αφετηρία). Η λεγόμενη και «θεϊκή αναλογία» στην Αναγέννηση ξεκίνησε ως μαθηματικός τύπος από τους Αρχαίους Ελληνες, με το ελληνικό γράμμα «φ» (από το πρώτο γράμμα του ονόματός του, αρχαίο γλύπτη Φειδία) να οδηγεί σε ένα αποτέλεσμα της εξίσωσης το 1,61803… Το νούμερο αυτό βέβαια, πέρα από τη μαθηματική και γεωμετρική του αξία, αναδείχθηκε και από τους καλλιτέχνες σε κάθε είδους, καθώς πιστεύεται ότι προσφέρει τη μεγαλύτερη αισθητική απόλαυση. Αν και θεωρείται -μάλλον αβάσιμα- ότι ήταν γνωστός και εφαρμοζόταν από τους αρχαίους χρόνους, ο κανόνας της χρυσής τομής έχει επηρεάσει δεκάδες καλλιτέχνες, από την Αναγέννηση μέχρι τις μέρες μας, ανάμεσά τους ο Νταλί στη ζωγραφική και ο Λε Κομρπυζιέ στην αρχιτεκτονική. Η σύνδεση της χρυσής τομής με αμέτρητα μοτίβα στη φύση προχωρούν ένα βήμα ακόμα τη μυστικιστική σχέση των μαθηματικών με τη δημιουργία του κόσμου.
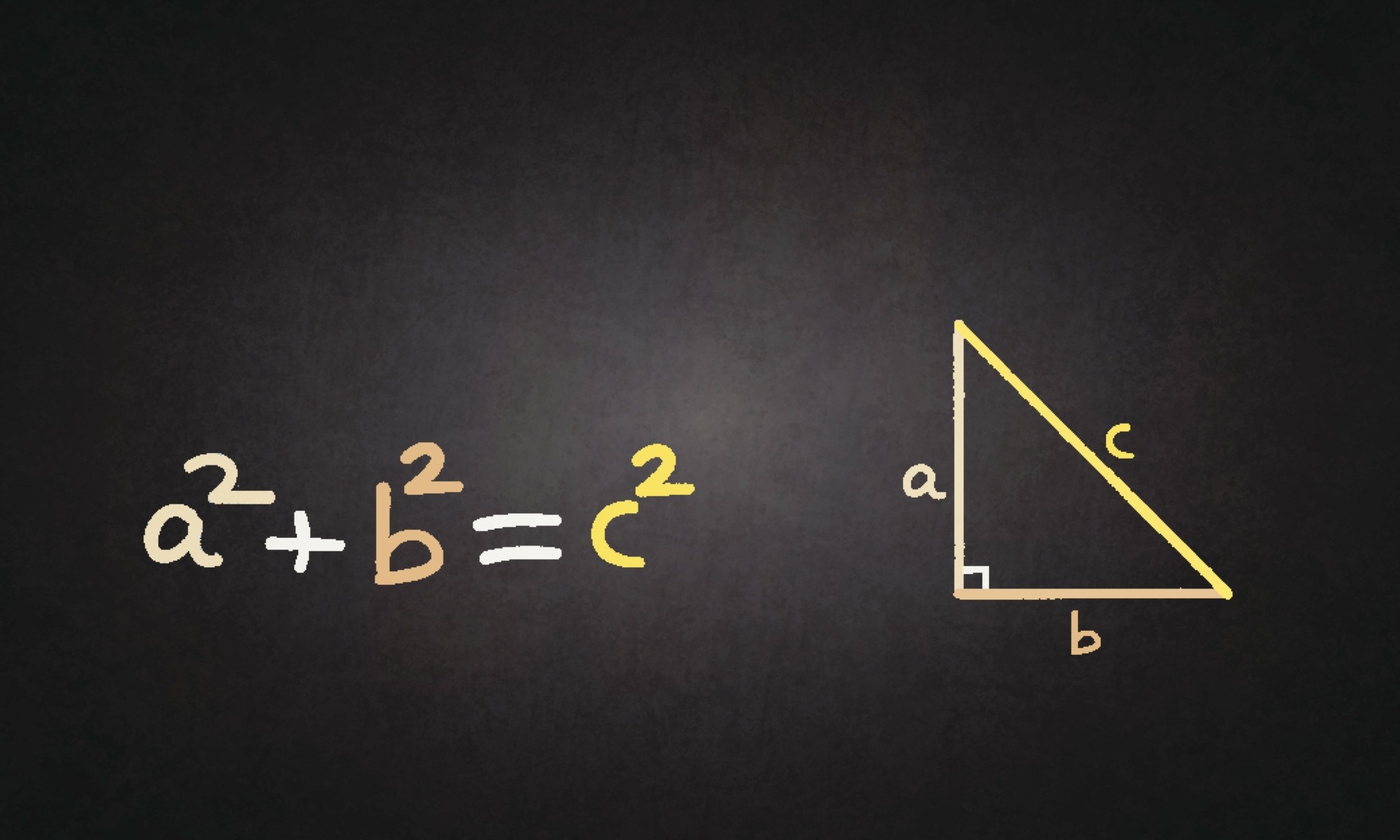
Το Πυθαγόρειο Θεώρημα
Το θεώρημα που ορίζει ότι σε ένα ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των δύο άλλων πλευρών. Αποδίδεται στον Πυθαγόρα, όμως υπάρχουν πολλές αμφιβολίες για το αν όντως ήταν αυτός που το διατύπωσε. Ο Πυθαγόρας υπήρξε κομβική μορφή στην εξέλιξη της Φιλοσοφίας της εποχής του, όμως ακόμα και σήμερα παραμένει ένα πρόσωπο με αμφιλεγόμενη παρουσία. Πολλοί θεωρούν ότι επρόκειτο για κάτι σαν γκουρού, με μεσσιανικά χαρακτηριστικά και θεωρίες επί παντός του επιστητού. Γύρω του είχε μαζέψει μια ομάδα νεαρών θαυμαστών που ονομάστηκαν Πυθαγόρειοι οι οποίοι μελετούσαν τις διδαχές του Πυθαγόρα, χτίζοντας μία φιλοσοφική σχολή που βασιζόταν στους αριθμούς.
Πολλοί υποστηρίζουν ότι το θεώρημα ήταν γνωστό από παλαιότερες εποχές σε λαούς όπως στους Αιγύπτιους και στους Βαβυλώνιους, όμως τελικά η απόδειξή του αποδίδεται στον Πυθαγόρα και έτσι έμεινε στην ιστορία με το όνομά του. Η καλλιτεχνική του αξία είναι προφανής, διαθέτοντας μία αισθητική αυτάρκεια και μία απλότητα που κάνει την ομορφιά της προσιτή σε όλους.
Διαβάστε ακόμη:
- Μάκης Βορίδης: Στον «Άγνωστο Στρατιώτη» δεν θα αναγράφεται τίποτε – Να σβηστούν τα ονόματα των θυμάτων των Τεμπών
- Τέμπη: «Η κόρη μου θεωρούσε το τρένο το πιο ασφαλές και κάηκε ζωντανή στους 1.400 βαθμούς»
- Ιωάννα Τούνη: Αγνώριστη μετά από την επέμβαση στη μύτη, πρησμένη και με μώλωπες – Βίντεο
- Ντρέα ντε Ματέο: Από το Sopranos, στο OnlyFans στα 51 της – Πώς άλλαξε η ζωή της και έσωσε το σπίτι της










